For my master’s thesis, I performed research on using Markov-chains with existing Wave Function Collapse(WFC) algorithms to improve on scalability while maintaining performance to allow for real-time procedural content generation using WFC.
Project Details
- Role: Systems Programmer
- Engine: Prodigy C++ Engine
- Development Time: 5 Months
- Language/Tools: C++ programming on the Prodigy Engine
Defense Presentation
Wave Function Collapse
Wave Function Collapse(WFC) is a constraint solving algorithm named after the quantum physics wave superposition concept. Maxim Gumin first implemented WFC using C# to incorporate a texture synthesis constraint solving PCG algorithm. By following a minimum entropy heuristic, the algorithm resolves constraints from a point on the output sample and propagates outwards resolving entropy to create a final pattern. These constraints determine the occurrence of specific information in the input data which can be visualized as neighboring pixel information in the case of 2D images. By splitting an image into some uniform chunks called Kernels, the WFC algorithm can identify patterns that exist in the input sample and their rate of occurrence. Using this information, WFC performs texture synthesis to generate a new output image that follows the same constraints observed in the input.
Here’s a GIF showing the algorithm’s constraint solving nature to resolve an output procedurally generated image:

Existing WFC Models
There are 2 models incorporated to generate procedural content using WFC, they are the Overlapping WFC (OWFC) and Tiling WFC (TWFC) models. In the case of 2D, the OWFC model splits an input image into smaller NxN sized kernels. These kernels are then overlapped to determine the possible occurrences of pixels in the output. The TWFC model, on the other hand, does not identify the kernels by splitting the input image into chunks, instead, it receives these kernels and their constraints in the form of meta-data. This meta-data can be used by TWFC to propagate constraints and solve the entropies of kernels without having to determine them in a pre-compute step. By eliminating the iterative kernel identification process, the TWFC model generates procedural outputs faster than the OWFC model. This, however, comes at the cost of manually generating a meta-data file that feeds the relevant constraint information to TWFC which is non-trivial, this affects the scalability of TWFC as increasing the complexity of the input can result in the need for increased investment of resources in determining the constraints required to generate desired results.
Overlapping Wave Function Collapse (OWFC)
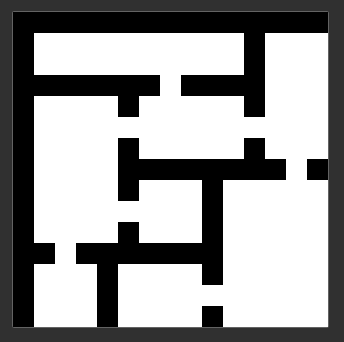
To perform the entropy resolution, an arbitrary pixel is selected in the output and assigned one of its possible color values. This reduces the entropy of that pixel to 1 and it is assigned 1 of the observed pixel colors. This information is then propagated to its neighboring pixels. Each of the neighboring pixels will check with observed kernels to determine what the possible colors could be for themselves given the previously resolved pixel with entropy 1. The check involves overlapping the kernel with the neighbor pixel to resolve to determine if the entropies for the neighbor pixel are valid based on the occurrences of pixels in the input.
The image below as an input provided to OWFC:


If a kernel refects the occurrence of the entropies on the neighbor pixel, the entropy is maintained, otherwise, all the options that are unlikely to occur are eliminated from the neighbor pixel. This results in the entropy of the neighbors either decreasing or remaining the same as before, this information is then propagated to its neighbors and the process continues recursively until all the pixels in the output image have been resolved to the entropy of 1. The recursive nature of OWFC occurs when entropy resolution on a pixel requires propagation of this information to all neighboring pixels, who will then need to propagate their manipulation to their neighboring pixels and so on.

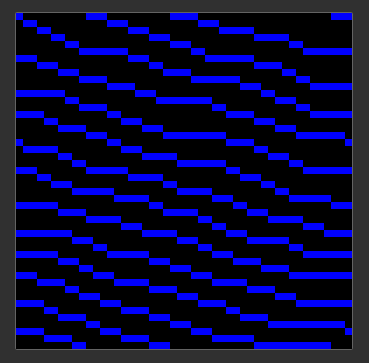
Due to the nature of the constraints used by the algorithm, there are instances where entropy resolution cannot resolve the output pixel entropies. This occurs when the constraints are either conflicting or there is not enough information to identify constraints that can resolve the output pixel entropy, in which case, WFC cannot generate a result with the provided input. However, it is interesting to note that with constraints on the symmetries permitted for the kernels, we can control the type of outputs. Here’s an example of the output generated when we don’t allow the kernels to reflect along the y-axis:

Here’s some of the logic involved in generating this image using OWFC:
//------------------------------------------------------------------------------------------------------------------------------
//Options needed for Overlapping WFC problem
struct OverlappingWFCOptions
{
bool m_periodicInput; // True if the input is toric(wrapping on x and y).
bool m_periodicOutput; // True if the output is toric(wrapping on x and y).
unsigned m_outHeight; // The height of the output in pixels.
unsigned m_outWidth; // The width of the output in pixels.
unsigned m_symmetry; // The number of symmetries (the order is defined in wfc).
bool m_ground; // True if the ground needs to be set (see InitializeGround).
unsigned m_patternSize; // The width and height in pixel of the patterns.
//get the wave height given these options
unsigned GetWaveHeight() const noexcept
{
return m_periodicOutput ? m_outHeight : m_outHeight - m_patternSize + 1;
}
//Get the wave width given these options
unsigned GetWaveWidth() const noexcept
{
return m_periodicOutput ? m_outWidth : m_outWidth - m_patternSize + 1;
}
};
//Return list of patterns as well as their probabilities of appearing
static std::pair<std::vector<Array2D<Color>>, std::vector<double>> GetPatterns(const Array2D<Color> &input, const OverlappingWFCOptions &options)
{
std::unordered_map<Array2D<Color>, uint> patterns_id;
std::vector<Array2D<Color>> patterns;
// The number of times a pattern is seen in the input image.
std::vector<double> patterns_weight;
std::vector<Array2D<Color>> symmetries(8, Array2D<Color>(options.m_patternSize, options.m_patternSize));
uint max_i = options.m_periodicInput ? input.m_height : input.m_height - options.m_patternSize + 1;
uint max_j = options.m_periodicInput ? input.m_width : input.m_width - options.m_patternSize + 1;
for (unsigned i = 0; i < max_i; i++)
{
for (unsigned j = 0; j < max_j; j++)
{
// Compute the symmetries of every pattern in the image.
symmetries[0].m_data = input.GetSubArray(i, j, options.m_patternSize, options.m_patternSize).m_data;
symmetries[1].m_data = symmetries[0].GetReflected().m_data;
symmetries[2].m_data = symmetries[0].GetRotated().m_data;
symmetries[3].m_data = symmetries[2].GetReflected().m_data;
symmetries[4].m_data = symmetries[2].GetRotated().m_data;
symmetries[5].m_data = symmetries[4].GetReflected().m_data;
symmetries[6].m_data = symmetries[4].GetRotated().m_data;
symmetries[7].m_data = symmetries[6].GetReflected().m_data;
// The number of symmetries in the option class define which symetries
// will be used.
for (uint k = 0; k < options.m_symmetry; k++)
{
//unordered map insert returns a pair of iterator and bool
std::pair<std::unordered_map<Array2D<Color>, uint>::iterator, bool> res;
res = patterns_id.insert(std::make_pair(symmetries[k], (uint)patterns.size()));
// If the pattern already exist, we just have to increase its number
// of appearance.
if (!res.second)
{
patterns_weight[res.first->second] += 1;
}
else
{
patterns.push_back(symmetries[k]);
patterns_weight.push_back(1);
}
}
}
}
return { patterns, patterns_weight };
}
//Precompute function IsPatternCompatibleWithThisPattern(pattern1, pattern2, dy, dx)
//If it returns true then pattern2 is compatible with pattern1 in the direction defined by dy, dx
//Add pattern2 to compatible[pattern1][direction]
static std::vector<std::array<std::vector<uint>, 4>> GenerateCompatible(const std::vector<Array2D<Color>> &patterns)
{
std::vector<std::array<std::vector<uint>, 4>> compatible = std::vector<std::array<std::vector<uint>, 4>>(patterns.size());
// Iterate on every dy, dx, pattern1 and pattern2
for (unsigned pattern1 = 0; pattern1 < patterns.size(); pattern1++)
{
for (unsigned direction = 0; direction < 4; direction++)
{
for (unsigned pattern2 = 0; pattern2 < patterns.size(); pattern2++)
{
if (IsPatternCompatibleWithThisPattern(patterns[pattern1], patterns[pattern2], directions_y[direction], directions_x[direction]))
{
compatible[pattern1][direction].push_back(pattern2);
}
}
}
}
return compatible;
}
Apart from having an OWFC class that handles all the information pertaining to OWFC, we also have a WFC class that performs entropy resolution based on constraints received, a WFC wave class which contains the generated output image as well as a WFC Propagator class which propagates the information across neighboring pixels as entropy resolution takes place.
Below is some of the logic involved observing the wave and propagating entropy resolution information to the wave:
enum ObserveStatus
{
SUCCESS, // WFC has finished and has succeeded.
FAILURE, // WFC has finished and failed.
TO_CONTINUE // WFC isn't finished.
};
//------------------------------------------------------------------------------------------------------------------------------
WFC::ObserveStatus WFC::Observe()
{
// Get the cell with lowest entropy.
int argmin = m_wave.GetMinEntropy(m_randomGenerator);
// If there is a contradiction, the algorithm has failed.
if (argmin == -2)
{
return FAILURE;
}
// If the lowest entropy is 0, then the algorithm has succeeded and
// finished.
if (argmin == -1)
{
WaveToOutput();
return SUCCESS;
}
// Choose an element according to the pattern distribution
double s = 0;
for (uint k = 0; k < m_numPatterns; k++)
{
s += m_wave.Get(argmin, k) ? m_patternFrequencies[k] : 0;
}
std::uniform_real_distribution<> dis(0, s);
double random_value = dis(m_randomGenerator);
uint chosen_value = m_numPatterns - 1;
for (uint k = 0; k < m_numPatterns; k++)
{
random_value -= m_wave.Get(argmin, k) ? m_patternFrequencies[k] : 0;
if (random_value <= 0)
{
chosen_value = k;
break;
}
}
// And define the cell with the pattern.
for (uint k = 0; k < m_numPatterns; k++)
{
if (m_wave.Get(argmin, k) != (k == chosen_value))
{
m_propagator.AddToPropagator(argmin / m_wave.width, argmin % m_wave.width, k);
m_wave.Set(argmin, k, false);
}
}
return TO_CONTINUE;
}
//------------------------------------------------------------------------------------------------------------------------------
void Propagator::Propagate(Wave &wave)
{
// We propagate every element while there is elements to propagate.
while (propagating.size() != 0)
{
// The cell and pattern that has been set to false.
uint y1, x1, pattern;
std::tie(y1, x1, pattern) = propagating.back();
propagating.pop_back();
// We propagate the information in all 4 directions.
for (uint direction = 0; direction < 4; direction++)
{
// We get the next cell in the direction direction.
int dx = directions_x[direction];
int dy = directions_y[direction];
int x2, y2;
if (periodic_output)
{
x2 = ((int)x1 + dx + (int)wave.width) % wave.width;
y2 = ((int)y1 + dy + (int)wave.height) % wave.height;
}
else
{
x2 = x1 + dx;
y2 = y1 + dy;
if (x2 < 0 || x2 >= (int)wave.width)
{
continue;
}
if (y2 < 0 || y2 >= (int)wave.height)
{
continue;
}
}
// The index of the second cell, and the patterns compatible
uint i2 = x2 + y2 * wave.width;
const std::vector<uint> &patterns = m_propagator_state[pattern][direction];
// For every pattern that could be placed in that cell without being in
// contradiction with pattern1
for (auto it = patterns.begin(), it_end = patterns.end(); it < it_end; ++it)
{
// We decrease the number of compatible patterns in the opposite
// direction If the pattern was discarded from the wave, the element
// is still negative, which is not a problem
std::array<int, 4> &value = compatible.Get(y2, x2, *it);
value[direction]--;
// If the element was set to 0 with this operation, we need to remove
// the pattern from the wave, and propagate the information
if (value[direction] == 0)
{
AddToPropagator(y2, x2, *it);
wave.Set(i2, *it, false);
}
}
}
}
}
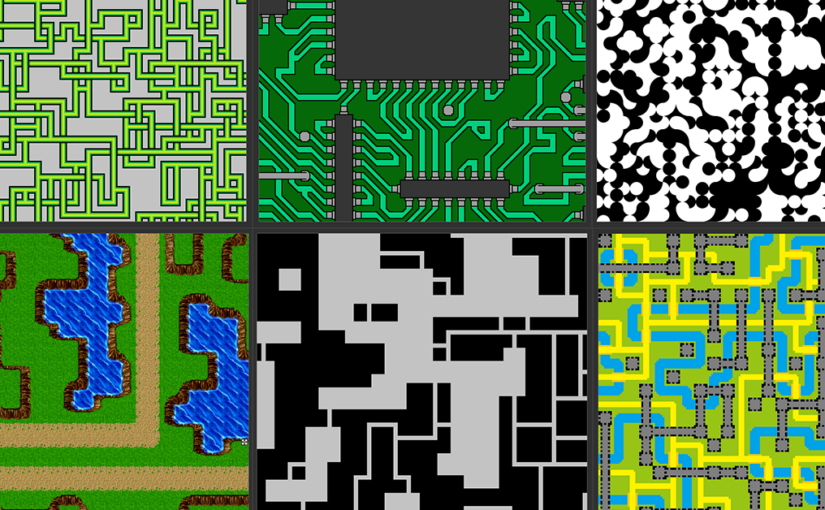
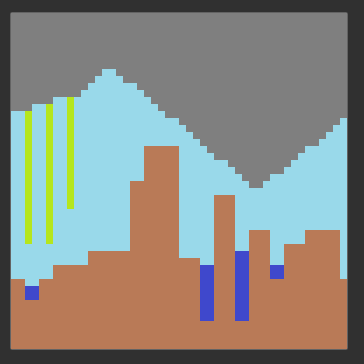
Here are some of the inputs tested with OWFC in our project:































Here are the corresponding outputs for the inputs highlighted above:






























Observations on OWFC
Below are some of the observations made when using OWFC to generate procedural results:
- The generated output will always follow rules determined from a provided input.
- The results of the algorithm are convincing as the constraint solving texture synthesis maintains the constraints in output.
- Execution time for OWFC is very high due to the iterative nature of the algorithm.
- Entropy resolution may not always take place in case there is too much detail in the image (i.e: Too many colors to resolve, too many intricate patterns to resolve for).
- There is very little control on the procedural-ness of the algorithm since the output is defined by the input sample, manipulating constraints can be very tricky.
Addressing the issues of OWFC
To address some of the performance problems with OWFC as well as to create scope for manipulating the procedural-ness of the algorithm, a Tiling WFC model was introduced. This model solves some of the problems of OWFC, by changing some of the inputs fed to the algorithm while maintaining the process involved in resolving the constraints used.
Tiling Wave Function Collapse (TWFC)
The TWFC model is very similar to the OWFC model except for the kernel generation step. Instead of computing the kernels present in an input sample, the TWFC model relies on a meta-data file that can provide the constraints required to generate an output image. By doing so, the tiling model can benefit from not having to use per-pixel entropies, instead, it can have a tile that can comprise some set of pixels that fit on a fixed tile grid. The constraints are neighborhood relationship information between 2 distinct tiles and their orientations. similar to OWFC, TWFC still requires the need to resolve the entropies of each tile in the output image as the WFC wave considers all tiles to have the highest possible entropies (i.e, the total number of tiles used by the algorithm) when generating the output.
Here’s an image illustrating the some of the tiles provided as input to TWFC and the corresponding outputs generated in different sizes:
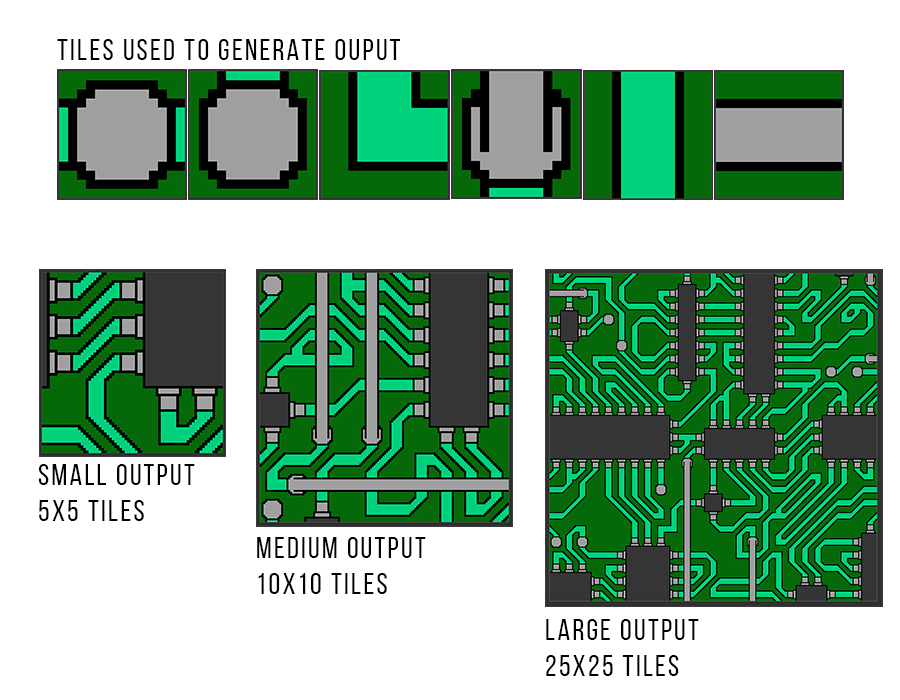
To achieve this, TWFC needed some changes in its logic, specifically using the constraints provided by meta-data as opposed to identifying said constraints from input sample images. This greatly reduces the time involved as there is no need to perform texture synthesis to infer constraint data.
Here’s some of the code showing how TWFC was implemented using a templated class:
//------------------------------------------------------------------------------------------------------------------------------
std::pair<uint, uint> FindTileAndMakeSymmetries(Array2D<T>& observedData)
{
//Check if any of the orientations of observedTile are part of m_tiles
std::pair<uint, uint> tileIDtoOrientation = std::make_pair(UINT_MAX, UINT_MAX);
bool foundTile = false;
for (uint tileIndex = 0; tileIndex < (uint)m_tiles.size(); tileIndex++)
{
//The m_tiles will have all orientations, just store the tile index and orientation index to determine tile we are
for (uint orientationIndex = 0; orientationIndex < NumPossibleOrientations(m_tiles[tileIndex].symmetry); orientationIndex++)
{
if (observedData == m_tiles[tileIndex].data[orientationIndex])
{
foundTile = true;
//Since we found the correct tile, it is safe to assume the observed tile has the same symmetry and data
tileIDtoOrientation.first = tileIndex;
tileIDtoOrientation.second = orientationIndex;
}
if (foundTile)
{
break;
}
}
if (foundTile)
{
break;
}
}
return tileIDtoOrientation;
}
//------------------------------------------------------------------------------------------------------------------------------
//Populate the neighbor information for the observed tile and observed neighbors
void PopulateNeighborRelationshipsForObservedTile(std::pair<uint, uint>& observedIDtoOrientation, std::vector< std::pair <std::pair<uint, uint>, NeighborType> > neighbors, std::vector< std::tuple<uint, uint, uint, uint> >& tileIDOrientationtoNeighborSet)
{
std::tuple<uint, uint, uint, uint> tileIDOrientationtoNeighbor;
uint observedOrientation;
uint neighborOrientation;
for (uint neighborIndex = 0; neighborIndex < neighbors.size(); neighborIndex++)
{
switch (neighbors[neighborIndex].second)
{
case RIGHT:
{
//Set the neighbor in it's current orientation
tileIDOrientationtoNeighbor = std::make_tuple(observedIDtoOrientation.first, observedIDtoOrientation.second, neighbors[neighborIndex].first.first, neighbors[neighborIndex].first.second);
AddObservedNeighborToNeighborsVector(tileIDOrientationtoNeighbor, tileIDOrientationtoNeighborSet);
continue;
}
case TOP:
{
//Get rotated three times for both observed tile and neighbor tile
observedOrientation = GetRotatedOrientationIDForObservedTile(observedIDtoOrientation, 3);
neighborOrientation = GetRotatedOrientationIDForObservedTile(neighbors[neighborIndex].first, 3);
tileIDOrientationtoNeighbor = std::make_tuple(observedIDtoOrientation.first, observedOrientation, neighbors[neighborIndex].first.first, neighborOrientation);
AddObservedNeighborToNeighborsVector(tileIDOrientationtoNeighbor, tileIDOrientationtoNeighborSet);
continue;
}
case LEFT:
{
//Get rotated twice for both observed tile and neighbor tile
observedOrientation = GetRotatedOrientationIDForObservedTile(observedIDtoOrientation, 2);
neighborOrientation = GetRotatedOrientationIDForObservedTile(neighbors[neighborIndex].first, 2);
tileIDOrientationtoNeighbor = std::make_tuple(observedIDtoOrientation.first, observedOrientation, neighbors[neighborIndex].first.first, neighborOrientation);
AddObservedNeighborToNeighborsVector(tileIDOrientationtoNeighbor, tileIDOrientationtoNeighborSet);
continue;
}
case BOTTOM:
{
//Get rotated once for both observed tile and neighbor tile
observedOrientation = GetRotatedOrientationIDForObservedTile(observedIDtoOrientation, 1);
neighborOrientation = GetRotatedOrientationIDForObservedTile(neighbors[neighborIndex].first, 1);
tileIDOrientationtoNeighbor = std::make_tuple(observedIDtoOrientation.first, observedOrientation, neighbors[neighborIndex].first.first, neighborOrientation);
AddObservedNeighborToNeighborsVector(tileIDOrientationtoNeighbor, tileIDOrientationtoNeighborSet);
continue;
}
}
}
}
//------------------------------------------------------------------------------------------------------------------------------
//Get the rotated tile orientation depending on tile symmetry
uint GetRotatedOrientationIDForObservedTile(const std::pair<uint, uint>& observedTileAndOrientation, uint numRotationsToPerform)
{
//Check the current tile's symmetry
Symmetry symmetry = m_tiles[observedTileAndOrientation.first].symmetry;
switch (symmetry)
{
case Symmetry::X:
{
//There is only 1 tile so just return 0
return 0;
}
case Symmetry::I:
case Symmetry::backslash:
{
//There are 2 possible tile orientations
return (observedTileAndOrientation.second + numRotationsToPerform) % 2;
}
case Symmetry::T:
case Symmetry::L:
{
//There are 4 possible tile orientations
return (observedTileAndOrientation.second + numRotationsToPerform) % 4;
}
case Symmetry::P:
{
//Special case where we have 8 possible outcomes
if (observedTileAndOrientation.second < 4)
{
//Normal case where we can add numRotations and mod by 4
return (observedTileAndOrientation.second + numRotationsToPerform) % 4;
}
else
{
//Special case where orientation is above 4
uint tempOrientation = observedTileAndOrientation.second;
tempOrientation -= 4;
tempOrientation += numRotationsToPerform;
tempOrientation %= 4;
tempOrientation += 4;
return tempOrientation;
}
}
default:
{
ERROR_AND_DIE("Couldn't find tile symmetry for the Markov problem to generate neighbors");
}
}
}
OWFC vs TWFC
When comparing the 2 models, OWFC model takes a sample image as input while the TWFC model takes a meta-data file as input which contains a set of tiles that can be used as subsets of the image or tiles that complete an image and some constraints that determine what tiles can be placed next to each other. By feeding the constraints and possible tiles in manually generated meta-data to TWFC, the kernel generation step is not required hence reducing the computational load involved of TWFC as opposed to that of OWFC. Since TWFC uses tiles on a fixed tile grid as opposed to pixels in an image, the user has control over the size of the tiles used as well as the complexity of the output generated as tiles can be simplified or made more detailed based on the user’s need. Unlike OWFC however, TWFC has no way of identifying the rate of occurrence for kernels (in this case tiles) occurring in input as there is no input image. Instead, to account for a rate of occurrence, TWFC requires this information to be some tile frequency or tile weight in the meta-data file.
Below is a sample meta-data used as input to TWFC.
<set size="32"> <tiles> <tile name="b_half" symmetry="T"/> <tile name="b_i" symmetry="I"/> <tile name="b_quarter" symmetry="L"/> <tile name="w_half" symmetry="T"/> <tile name="w_i" symmetry="I"/> <tile name="w_quarter" symmetry="L"/> <tile name="b" symmetry="X"/> <tile name="w" symmetry="X"/> </tiles> <neighbors> <neighbor left="b_half" right="b_half"/> <neighbor left="b_half 1" right="b_half 3"/> <neighbor left="b_half 3" right="b_half 1"/> <neighbor left="b_half" right="b_half 3"/> <neighbor left="b_half" right="b_half 2"/> <neighbor left="b_half" right="b_i"/> <neighbor left="b_half 3" right="b_i 1"/> <neighbor left="b_half 1" right="b_i"/> <neighbor left="b_half" right="b_quarter"/> <neighbor left="b_half 1" right="b_quarter"/> <neighbor left="b_half 2" right="b_quarter"/> <neighbor left="b_half 3" right="b_quarter 1"/> <neighbor left="b_i" right="b_i"/> <neighbor left="b_i 1" right="b_i 1"/> <neighbor left="b_i" right="b_quarter"/> <neighbor left="b_i 1" right="b_quarter 1"/> <neighbor left="b_quarter" right="b_quarter 1"/> <neighbor left="b_quarter 1" right="b_quarter"/> <neighbor left="b_quarter 2" right="b_quarter"/> <neighbor left="b_quarter" right="b_quarter 2"/> <neighbor left="b_half 1" right="w_half 1"/> <neighbor left="b_half" right="w_half 1"/> <neighbor left="b_half 3" right="w_half"/> <neighbor left="b_half 3" right="w_half 3"/> <neighbor left="b_half" right="w_i 1"/> <neighbor left="b_half 1" right="w_i 1"/> <neighbor left="b_half 3" right="w_i"/> <neighbor left="b_half" right="w_quarter 1"/> <neighbor left="b_half" right="w_quarter 2"/> <neighbor left="b_half 1" right="w_quarter 1"/> <neighbor left="b_half 3" right="w_quarter"/> <neighbor left="b_i" right="w_half 1"/> <neighbor left="b_i 1" right="w_half"/> <neighbor left="b_i 1" right="w_half 3"/> <neighbor left="b_i" right="w_i 1"/> <neighbor left="b_i 1" right="w_i"/> <neighbor left="b_i" right="w_quarter 1"/> <neighbor left="b_i 1" right="w_quarter"/> <neighbor left="b_quarter" right="w_half"/> <neighbor left="b_quarter" right="w_half 3"/> <neighbor left="b_quarter" right="w_half 2"/> <neighbor left="b_quarter 1" right="w_half 1"/> <neighbor left="b_quarter" right="w_i"/> <neighbor left="b_quarter 1" right="w_i 1"/> <neighbor left="b_quarter" right="w_quarter"/> <neighbor left="b_quarter" right="w_quarter 3"/> <neighbor left="b_quarter 1" right="w_quarter 1"/> <neighbor left="b_quarter 1" right="w_quarter 2"/> <neighbor left="w_half" right="w_half"/> <neighbor left="w_half 1" right="w_half 3"/> <neighbor left="w_half 3" right="w_half 1"/> <neighbor left="w_half" right="w_half 3"/> <neighbor left="w_half" right="w_half 2"/> <neighbor left="w_half" right="w_i"/> <neighbor left="w_half 3" right="w_i 1"/> <neighbor left="w_half 1" right="w_i"/> <neighbor left="w_half" right="w_quarter"/> <neighbor left="w_half 1" right="w_quarter"/> <neighbor left="w_half 2" right="w_quarter"/> <neighbor left="w_half 3" right="w_quarter 1"/> <neighbor left="w_i" right="w_i"/> <neighbor left="w_i 1" right="w_i 1"/> <neighbor left="w_i" right="w_quarter"/> <neighbor left="w_i 1" right="w_quarter 1"/> <neighbor left="w_quarter" right="w_quarter 1"/> <neighbor left="w_quarter 1" right="w_quarter"/> <neighbor left="w_quarter 2" right="w_quarter"/> <neighbor left="w_quarter" right="w_quarter 2"/> <neighbor left="b" right="b"/> <neighbor left="b" right="b_half 1"/> <neighbor left="b" right="b_i 1"/> <neighbor left="b" right="b_quarter 1"/> <neighbor left="b" right="w_half"/> <neighbor left="b" right="w_half 3"/> <neighbor left="b" right="w_i"/> <neighbor left="b" right="w_quarter"/> <neighbor left="w" right="w"/> <neighbor left="w" right="w_half 1"/> <neighbor left="w" right="w_i 1"/> <neighbor left="w" right="w_quarter 1"/> <neighbor left="w" right="b_half"/> <neighbor left="w" right="b_half 3"/> <neighbor left="w" right="b_i"/> <neighbor left="w" right="b_quarter"/> </neighbors> </set>
Getting to the point of all this
Markov-Chain WFC Model
The proposed Markov-chain WFC (MkWFC) model aims to solve the scalability issues of TWFC while maintaining the performance benefits it provides over OWFC. TWFC provides an advantage of reducing the computational overhead of OWFC by using manually generated meta-data that defines the various neighborhood tile relationships. The non-trivial manual generation of the meta-data however, affects the scalability of TWFC with either addition or deletion of tiles. To eliminate this scalability tradeoff, MkWFC performs an automation step to infer the constraints rather than use a manually generated meta-data file. Instead, MkWFC uses the tile information to observe some input images provided in meta-data to determine constraints that would be used by TWFC. Although this introduces an overhead in terms of execution time, by automating the non-trivial step of constraint identification, MkWFC simplifies the meta-data required making the algorithm scalable.
Below is an example of the meta-data fed as input to MkWFC:
<set size="32"> <tiles> <tile name="b_half" symmetry="T"/> <tile name="b_i" symmetry="I"/> <tile name="b_quarter" symmetry="L"/> <tile name="w_half" symmetry="T"/> <tile name="w_i" symmetry="I"/> <tile name="w_quarter" symmetry="L"/> <tile name="b" symmetry="X"/> <tile name="w" symmetry="X"/> </tiles> <inputs> <input name="MarkovInputImage1" /> <input name="MarkovInputImage2" /> <input name="MarkovInputImage3" /> </inputs> </set>
By simplifying the meta-data being used, we are able to eliminate the non-trivial meta-data data generation process of having to determine the constraints manually. Instead, the MkWFC model uses the kernel identification advantages of OWFC, while maintaining the control and performance advantages of TWFC.
This meant that we needed to do the tiling logic and use of symmetry the same way that TWFC would do it but add an extra step of identifying the constraints required by WFC from some input samples which are defined in the meta-data.
Below is the code I implemented to generate the WFC Propagator and to infer neighborhood constraints from a set of images having known the tiles being used and their fixed size beforehand.
//Generate the propagator which will be used in the wfc algorithm
static std::vector<std::array<std::vector<uint>, 4>> GeneratePropagator(
const std::vector<std::tuple<uint, uint, uint, uint>>
&neighbors,
std::vector<Tile<T>> tiles,
std::vector<std::pair<uint, uint>> id_to_oriented_tile,
std::vector<std::vector<uint>> oriented_tile_ids)
{
size_t nb_oriented_tiles = id_to_oriented_tile.size();
std::vector<std::array<std::vector<bool>, 4>> dense_propagator(
nb_oriented_tiles, { std::vector<bool>(nb_oriented_tiles, false),
std::vector<bool>(nb_oriented_tiles, false),
std::vector<bool>(nb_oriented_tiles, false),
std::vector<bool>(nb_oriented_tiles, false) });
for (auto neighbor : neighbors)
{
uint tile1 = std::get<0>(neighbor);
uint orientation1 = std::get<1>(neighbor);
uint tile2 = std::get<2>(neighbor);
uint orientation2 = std::get<3>(neighbor);
std::vector<std::vector<uint>> action_map1 = Tile<T>::GenerateActionMap(tiles[tile1].symmetry);
std::vector<std::vector<uint>> action_map2 = Tile<T>::GenerateActionMap(tiles[tile2].symmetry);
auto add = [&](uint action, uint direction)
{
uint temp_orientation1 = action_map1[action][orientation1];
uint temp_orientation2 = action_map2[action][orientation2];
uint oriented_tile_id1 = oriented_tile_ids[tile1][temp_orientation1];
uint oriented_tile_id2 = oriented_tile_ids[tile2][temp_orientation2];
dense_propagator[oriented_tile_id1][direction][oriented_tile_id2] = true;
direction = GetOppositeDirection(direction);
dense_propagator[oriented_tile_id2][direction][oriented_tile_id1] = true;
};
add(0, 2);
add(1, 0);
add(2, 1);
add(3, 3);
add(4, 1);
add(5, 3);
add(6, 2);
add(7, 0);
}
std::vector<std::array<std::vector<uint>, 4>> propagator(nb_oriented_tiles);
for (size_t i = 0; i < nb_oriented_tiles; ++i)
{
for (size_t j = 0; j < nb_oriented_tiles; ++j)
{
for (size_t d = 0; d < 4; ++d)
{
if (dense_propagator[i][d][j])
{
propagator[i][d].push_back((uint)j);
}
}
}
}
return propagator;
}
//Get probability of presence of tiles
static std::vector<double> GetTilesWeight(const std::vector<Tile<T>> &tiles)
{
std::vector<double> frequencies;
for (size_t i = 0; i < tiles.size(); ++i)
{
for (size_t j = 0; j < tiles[i].data.size(); ++j)
{
frequencies.push_back(tiles[i].weight / tiles[i].data.size());
}
}
return frequencies;
}
//------------------------------------------------------------------------------------------------------------------------------
//Infer neighbors for the Markov WFC Problem
std::vector<std::tuple<uint, uint, uint, uint>> InferNeighbors()
{
m_initTime = GetCurrentTimeSeconds();
std::vector<std::tuple<uint, uint, uint, uint> > neighborSet;
for (uint inputIndex = 0; inputIndex < m_inputs.size(); inputIndex++)
{
//Identify all pixels and turn them into a 2D array of tile ID and orientations
uint xIndex = 0;
uint yIndex = 0;
while (xIndex != m_inputs[inputIndex].m_width && yIndex != m_inputs[inputIndex].m_height)
{
Array2D<T> observedData = Array2D<T>(m_options.m_tileSize, m_options.m_tileSize);
Array2D<T> observedNeighborData = Array2D<T>(m_options.m_tileSize, m_options.m_tileSize);
observedData = m_inputs[inputIndex].GetSubArray(yIndex, xIndex, m_options.m_tileSize, m_options.m_tileSize);
//Find the tile in the set and get the correct Tile object with the correct symmetries and weights
std::pair<uint, uint> observedIDtoOrientation = FindTileAndMakeSymmetries(observedData);
if (observedIDtoOrientation.first == UINT_MAX)
{
ERROR_AND_DIE("ERROR! pattern observed does not correspond to any tile for Markov Problem");
}
//Find all the 4 neighbors for the tile
std::vector< std::pair <std::pair<uint, uint>, NeighborType> > neighbors = FindNeighborsForTileAtPosition(xIndex, yIndex, m_options.m_tileSize, m_inputs[inputIndex]);
//Generate relationships for the top, left, right and bottom tiles when generating neighbor information for the markov set
PopulateNeighborRelationshipsForObservedTile(observedIDtoOrientation, neighbors, neighborSet);
//Step ahead by tile size
xIndex += m_options.m_tileSize;
if (xIndex == m_inputs[inputIndex].m_width)
{
yIndex += m_options.m_tileSize;
xIndex = 0;
}
}
}
m_neighborGenerationTime = GetCurrentTimeSeconds() - m_initTime;
m_numPermutations = (int)neighborSet.size();
return neighborSet;
}
//------------------------------------------------------------------------------------------------------------------------------
std::vector< std::pair <std::pair<uint, uint>, NeighborType> > FindNeighborsForTileAtPosition(uint xIndex, uint yIndex, uint tileSize, const Array2D<T>& inputImage)
{
std::vector< std::pair <std::pair<uint, uint> , NeighborType> > neighbors;
std::pair<uint, uint> tileIDandOrientation = std::make_pair(UINT_MAX, UINT_MAX);
Array2D<T> tempTileArray(tileSize, tileSize);
bool validationResult = false;
//Get the right neighbor
validationResult = ValidateIndicesForSubArrayGet(yIndex, xIndex + tileSize, inputImage.m_height, inputImage.m_width, tileSize);
if (validationResult)
{
tempTileArray = inputImage.GetSubArrayNonToric(yIndex, xIndex + tileSize, tileSize, tileSize);
PopulateNeighbor(tempTileArray, neighbors, RIGHT);
}
//get the btoom neighbor
validationResult = ValidateIndicesForSubArrayGet(yIndex + tileSize, xIndex, inputImage.m_height, inputImage.m_width, tileSize);
if (validationResult)
{
tempTileArray = inputImage.GetSubArrayNonToric(yIndex + tileSize, xIndex, tileSize, tileSize);
PopulateNeighbor(tempTileArray, neighbors, BOTTOM);
}
//get the left neighbor
validationResult = ValidateIndicesForSubArrayGet(yIndex, xIndex - tileSize, inputImage.m_height, inputImage.m_width, tileSize);
if (validationResult)
{
tempTileArray = inputImage.GetSubArrayNonToric(yIndex, xIndex - tileSize, tileSize, tileSize);
PopulateNeighbor(tempTileArray, neighbors, LEFT);
}
//get the top neighbor
validationResult = ValidateIndicesForSubArrayGet(yIndex - tileSize, xIndex, inputImage.m_height, inputImage.m_width, tileSize);
if (validationResult)
{
tempTileArray = inputImage.GetSubArrayNonToric(yIndex - tileSize, xIndex, tileSize, tileSize);
PopulateNeighbor(tempTileArray, neighbors, TOP);
}
return neighbors;
}
The automation of kernel neighborhood (constraint) determination makes MkWFC a more scalable model with varying sizes. Here are some of the results we found when comparing TWFC with MkWFC with different input and output sizes:
| Percentage Increase of identified constraints | |
| Mean | 2.940175311 |
| Standard Error | 0.184370112 |
| Median | 2.802396474 |
| Mode | N/A |
| Standard Deviation | 0.451612697 |
| Sample Variance | 0.203954028 |
| Kurtosis | 4.7133119 |
| Skewness | 2.044242767 |
| Range | 1.289060791 |
| Minimum | 2.539970812 |
| Maximum | 3.829031603 |
| Sum | 17.64105187 |
| Count | 6 |
| Confidence Level (95%) | 0.47393846 |
These results indicate that there was an average of 294% increase in the number of constraints identified by MkWFC as opposed to TWFC. The table also shows that at minimum the increase was 253% with a maximum increase of 382% more constraints identified by MkWFC. From this data, we can infer that MkWFC can do better than TWFC in all cases when identifying constraint information from a set of input sample images as opposed to curating the meta-data manually.
Below is an image highlighting all the different outputs we received when solving with MkWFC as well as their corresponding inputs used. As can be seen, the images follow the rules in the input and procedurally generate outputs that fit into those constraints similar to TWFC, except in the case of MkWFC, these constraints are inferred from the image.

Interesting results and side effects of MkWFC
When running the trials highlighted above using MkWFC and comparing the performance against TWFC, there was some interesting phenomenon worth noting. One of the interesting phenomena was that due to the increase in coverage with the MkWFC model, the number of constraints read would be almost double that of TWFC which will result in the increase of coverage of constraints in the output. However, this also introduces a greater scope for conflicting constraints like in the case of generating circuits where sometimes the output wave would not be able to resolve entropies per pixel to a final value of 1 due to adjacency constraint conflict.
Another side effect of reading increased constraints is the emergence of constraints that would not otherwise exist in TWFC. This can be observed in the case of generating Castles (2nd problem from bottom in the previous image) where MkWFC will seemingly place towers at random positions, hence compromising the structure of the castle on the map. This may at first be considered a bug with the algorithm but is actually a valid output due to constraint identification allowing the placement of castles next to the adjacency scenarios exhibited by the neighboring tiles on the map. This can result in some constraints being observed in the input that may hamper the desired results of MkWFC.
Retrospectives
What went well 🙂
- Implementation of OWFC and TWFC models was done early using solid references to ensure the comparison model was in place.
- Clearly able to identify the metrics that needed to be measured for the proposed model.
- MkWFC performs as expected with given constraints.
- Debug tests with small inputs and small outputs before adding complexity to the pipeline.
What went wrong 🙁
- Inefficient iterative check-in MkWFC model that does some repetition on the input sample during constraint identification.
- Logging was done inefficiently which took up too much time during data analysis.
- The project should have accounted for the need to compare large sets of data and built a .csv structure to simplify the analysis part.
What I would do differently next time 🙂
- Solid logging system capable of handling a variety of data collection needs
- Added more automated control scripts that can execute the desired runs under desired conditions
- Added a simple UI to allow for check-box options to toggle specific things on and off